Верховна Рада проти статистики. Депутати тюхтії чи зрадники?
Як за допомогою комп'ютера оцінити ймовірність змови під час голосування. Хоча ми пишемо про конкретний випадок, подібну перевірку можна зробити для будь-якого "серійного" голосування у ВР.Нагадаємо, що 26 січня депутати сім разів поспіль голосували за один законопроект, але так його і не прийняли.
Автор: Анатолій Бондаренко
Законопроект був цікавий з двох причин - по перше, через свою скандальність (депутати затягують час, щоб не приймати закон про обов'язкові електронні декларації), а по друге - якби зібрати всі голоси "за" у цій серії голосувань, то він би пройшов.
Проте значна частина депутатів декілька разів змінювали свою точку зору протягом дуже короткого часу. У нас виникло питання - що це було, неорганізованість чи небажання приймати закон? Для частини депутатів важливо не показати, що вони відкрито саботують антикорупційні ініціативи. Теоретично, це можна робити змінюючи своє голосування залежно від попередніх результатів або від того, як голосують твої сусіди.
Власне, далі ми розкажемо про те, як визначити - звичайно, із долею ймовірності - чи була ця серія голосувань "змовою", чи законопроект №3755 депутати не змогли прийняти випадково.
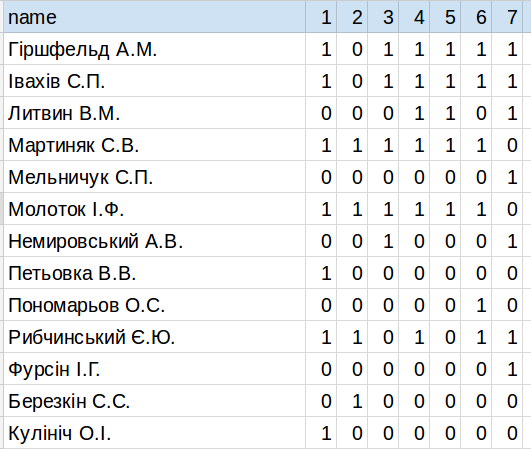
Отже, ми будемо працювати лише з тими депутатами, які хоча би раз підтримали законопроект у серії з семи голосувань. Тих, що не дали своїх голосів за нього (або голосували проти), а також тих, що весь час голосували за, ми розглядати не будемо, у даному випадку вони не впливають на нашу перевірку. Отже, було 88 депутатів, які хоча би раз проголосували "за".
Як вони голосували, дивіться y таблиці
Для ілюстрації, наводимо фрагмент:
Якщо депутати не хотіли прийняти законопроект, але водночас бажали зімітувати підтримку, тоді їх мета - давати голоси в якомусь діапазоні - трохи менше голосів, ніж потрібно для прийняття, але більше якогось порогу, щоб їх не можна було звинуватити у захисті корупційних практик.
Максимальна кількість голосів, яка дала ця група - 57.
Мінімальна кількість - 47.
Отже, назвем це обмеженням-1: кількість голосів лежить в інтервалі (47, 57).
Головна ідея перевірки, чи було це голосування змовою, чи все вийшло випадково, наступна:
- якщо депутат не намагався підігнати результат під обмеження-1, то ми можемо брати його голоси у будь якій послідовності: скажімо не голоси в 1,2,3 ... 7 стовпчиках в таблиці голосування на Мал.1, а наприклад 2,1,5,7,4,3,6 - і так для кожного з таблиці (іншими словами, ми будемо перемішувати (або, як говорять математики, робити перестановку) голосів у кожному рядку таблиці). У такому випадку,кожне наступне голосування депутата не залежить від його попередніх голосувань (та від попередніх загальних результатів) - тобто, ми відкидаємо таким чином варіант його участі у "змові".
Після подібного перемішування, ми можемо порахувати - скільки голосів отримує законопроект у кожному з семи голосувань. І повторимо це, скажімо, тисячу разів. Після цього виберемо з результатів лише ті, які підходять під реальний результат, під наше обмеження-1 (нагадаю, це значить що всі голосування мають бути не менше ніж 47, і не більше ніж 57 голосів "за").
Частка голосувань, що підходить під такі умови, буде імовірністю, що змови не було (зазвичай наукові дослідження приймають гіпотезу "змови", якщо ця частка менше 0.05, або 5%)
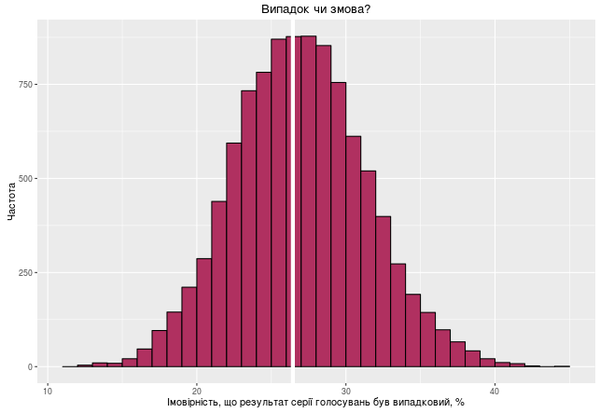
Однак, ми можемо зробити ще краще, і провести описане вище обчислення (симуляцію), багато разів - скажімо, 10000. Запишемо результат (частку голосувань, що підходить під обмеження-1) у таблицю з 10000 строк і побудуємо функцію розподілу для цієї величини.
Таким чином ми не лише отримаємо імовірність того, що реальний результат голосувань не є наслідком "змови", але ще й зможемо оцінити похибку цієї ймовірності.
Результат подібного моделювання - на малюнку нижче. Середнє значення - 26.4%, стандартне відхилення - 4.4. Тобто, найбільш ймовірний інтервал, куди потрапляє більшість значень цієї величини - приблизно від 18 до 37%.
Висновки: ймовірність того, що отримані в реальності результати голосування є випадковими, складає 26% (менше ніж 50%) і шанси на "зраду" таким чином десь 3 до 1.
Водночас, статистично ми не можемо остаточно відкинути гіпотезу, що реальні результати голосування у тій серії виникли внаслідок випадку (для того щоб відкинути таку гіпотезу, підрахована нами ймовірність повинна бути значно менше 5%).
А значить, довести для цього голосування, що змова таки була, - нам не вдалося (водночас, це не означає що її не було - ми просто не можемо довести її наявність).
Депутати, які то голосували, то ні, не зрадники, вони тюхтії.